I. Einleitung
Kann man Kerzen mit Wasser anzünden? Stimmt das? Ja, es stimmt!
Stimmt es, dass Schlangen Angst vor Realgar haben? Das ist falsch!
Was wir heute besprechen werden, ist Folgendes:
Störungen können die Messgenauigkeit verbessern, stimmt das?
Unter normalen Umständen ist Störung der natürliche Feind von Messungen. Sie verringert die Messgenauigkeit und kann in schweren Fällen nicht ordnungsgemäß durchgeführt werden. Aus dieser Perspektive betrachtet, kann Störung die Messgenauigkeit verbessern – das ist jedoch falsch!
Ist das jedoch immer der Fall? Gibt es Situationen, in denen Störungen die Messgenauigkeit nicht verringern, sondern im Gegenteil verbessern?
Die Antwort lautet ja!
2. Interferenzvereinbarung
Unter Berücksichtigung der tatsächlichen Situation treffen wir folgende Vereinbarung bezüglich der Störung:
- Die Störungen enthalten keine Gleichstromkomponenten. Bei der tatsächlichen Messung handelt es sich bei den Störungen hauptsächlich um Wechselstromstörungen, und diese Annahme ist gerechtfertigt.
- Im Vergleich zur gemessenen Gleichspannung ist die Störamplitude relativ gering. Dies entspricht der Realität.
- Störungen sind periodische Signale, deren Mittelwert innerhalb eines festgelegten Zeitraums null ist. Dies trifft in der Praxis nicht immer zu. Da es sich bei Störungen jedoch im Allgemeinen um hochfrequente Wechselstromsignale handelt, ist die Annahme eines Mittelwerts von null für die meisten Störungen über einen längeren Zeitraum hinweg sinnvoll.
3. Messgenauigkeit unter Störungen
Die meisten elektrischen Messgeräte und -instrumente verwenden heutzutage AD-Wandler, deren Messgenauigkeit eng mit der Auflösung des AD-Wandlers zusammenhängt. Generell gilt: Je höher die Auflösung des AD-Wandlers, desto höher die Messgenauigkeit.
Die Auflösung des AD-Wandlers ist jedoch stets begrenzt. Angenommen, die Auflösung beträgt 3 Bit und die maximale Messspannung 8 V, so entspricht der AD-Wandler einer Skala, die in 8 Abschnitte unterteilt ist, wobei jeder Abschnitt 1 V entspricht. Das Messergebnis dieses AD-Wandlers ist immer eine ganze Zahl, wobei der Dezimalteil entweder überschrieben oder verworfen wird. In dieser Arbeit wird von einem Übertrag ausgegangen. Überschreiben oder Verwerfen führt zu Messfehlern. Beispielsweise ist 6,3 V größer als 6 V und kleiner als 7 V. Das AD-Messergebnis beträgt 7 V, was einen Fehler von 0,7 V ergibt. Dieser Fehler wird als AD-Quantisierungsfehler bezeichnet.
Zur Vereinfachung der Analyse gehen wir davon aus, dass die Waage (AD-Wandler) außer dem AD-Quantisierungsfehler keine weiteren Messfehler aufweist.
Nun verwenden wir zwei solche identischen Skalen, um die beiden in Abbildung 1 dargestellten Gleichspannungen ohne Störungen (ideale Situation) und mit Störungen zu messen.
Wie in Abbildung 1 dargestellt, beträgt die gemessene Gleichspannung 6,3 V. Die Gleichspannung im linken Diagramm ist störungsfrei und konstant. Das rechte Diagramm zeigt den durch Wechselstrom gestörten Gleichstrom mit entsprechenden Schwankungen. Nach Entfernung des Störsignals entspricht die Gleichspannung im rechten Diagramm der Gleichspannung im linken Diagramm. Das rote Quadrat in der Abbildung stellt das Ergebnis der AD-Wandler-Umwandlung dar.

Ideale Gleichspannung ohne Störungen
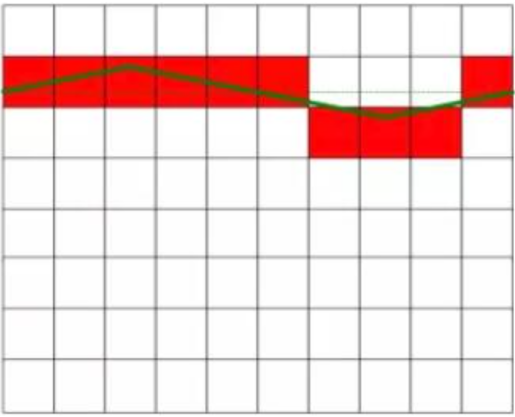
Legen Sie eine Störspannung mit einem Mittelwert von Null an.
Nehmen Sie in den beiden Fällen in der obigen Abbildung jeweils 10 Messungen des Gleichstroms vor und bilden Sie dann den Mittelwert der 10 Messungen.
Die erste Skala links wurde zehnmal gemessen, wobei die Messwerte jedes Mal gleich waren. Aufgrund des Quantisierungsfehlers der AD-Wandlung betrug jeder Messwert 7 V. Auch nach Mittelung der zehn Messungen ergab sich ein Wert von 7 V. Der Quantisierungsfehler der AD-Wandlung und der Messfehler betragen jeweils 0,7 V.
Die zweite Skala auf der rechten Seite hat sich dramatisch verändert:
Aufgrund der unterschiedlichen Vorzeichen und Amplituden der Störspannung variiert der AD-Quantisierungsfehler an verschiedenen Messpunkten. Mit der Änderung des AD-Quantisierungsfehlers schwankt das AD-Messergebnis zwischen 6 V und 7 V. Sieben Messungen ergaben 7 V, nur drei 6 V, und der Mittelwert der zehn Messungen betrug 6,3 V! Der Fehler ist also null!
Tatsächlich ist kein Fehler unmöglich, denn in der objektiven Welt gibt es keine strikten 6,3 V! Es gibt jedoch sehr wohl:
Im Falle keiner Störung, da jedes Messergebnis gleich ist, bleibt der Fehler nach Mittelung von 10 Messungen unverändert!
Bei ausreichendem Störanteil wird der AD-Quantisierungsfehler nach Mittelung von 10 Messungen um eine Größenordnung reduziert! Die Auflösung verbessert sich um eine Größenordnung! Auch die Messgenauigkeit verbessert sich um eine Größenordnung!
Die Schlüsselfragen lauten:
Gilt das Gleiche auch für andere gemessene Spannungswerte?
Leser können der Vereinbarung zur Interferenz im zweiten Abschnitt folgen, die Interferenz durch eine Reihe numerischer Werte ausdrücken, die Interferenz der gemessenen Spannung überlagern und dann die Messergebnisse jedes Punktes gemäß dem Übertragungsprinzip des AD-Wandlers berechnen und anschließend den Mittelwert zur Überprüfung berechnen. Solange die Interferenzamphung eine Änderung des Messwerts nach der AD-Quantisierung bewirken kann und die Abtastfrequenz hoch genug ist (die Änderung der Interferenzamphung weist einen Übergangsprozess auf und nicht nur zwei positive und negative Werte), muss die Genauigkeit verbessert werden!
Es lässt sich beweisen, dass, solange die gemessene Spannung keine exakte ganze Zahl ist (was in der Realität nicht der Fall ist), ein AD-Quantisierungsfehler auftritt. Unabhängig von der Größe dieses Fehlers führt eine Störungsamplitude, die größer als der Fehler oder die minimale Auflösung des AD-Wandlers ist, zu einer Änderung des Messergebnisses zwischen zwei benachbarten Werten. Da die Störung positiv und negativ symmetrisch ist, sind Betrag und Wahrscheinlichkeit für eine Abnahme bzw. Zunahme gleich. Daher ist die Wahrscheinlichkeit für das Auftreten eines bestimmten Wertes am größten, wenn der tatsächliche Wert nahe an diesem liegt. Nach der Mittelung liegt der Messwert dann nahe an diesem Wert.
Das heißt: Der Mittelwert mehrerer Messungen (Interferenzmittelwert ist Null) muss näher am Messergebnis ohne Interferenz liegen, d. h. die Verwendung des AC-Interferenzsignals mit einem Mittelwert von Null und die Mittelung mehrerer Messungen können die äquivalenten AD-Quantisierungsfehler reduzieren, die AD-Messauflösung verbessern und die Messgenauigkeit erhöhen!
Veröffentlichungsdatum: 13. Juli 2023




